Toda la información que necesitas sobre el Teorema de Bolzano
Conocer los diversos teoremas y cálculos matemáticos no es para cualquiera. Si no estás metido en el mundo ni eres muy amante de los números, hacer esto se puede volver un trabajo muy, pero muy pesado y complicar tu TFG, TFM o tesis doctoral (TD). En este artículo te explicaremos qué es el Teorema de Bolzano, para qué sirve y cómo aplicarlo correctamente.
¿Qué es el Teorema de Bolzano?
El Teorema de Bolzano es una hipótesis matemática que se utiliza para trazar los gráficos de funciones continuas que se definen sobre un intervalo de dos ejes. Por medio del mismo, se puede demostrar o probar que existen soluciones en ecuaciones de funciones continuas y reales. Eso dentro de intervalos con valores positivos y negativos. Es de los modelos más aplicados para hallar la solución de varias ecuaciones.
La tesis que sustenta el Teorema de Bolzano sostiene que, en algún momento del intervalo, la función se anula. Uno de los requisitos que debe cumplir el teorema es que los signos deben ser contrarios. No obstante, para ello también debes conocer la ley de los signos.
¿Qué es una función continua y real?
Una función continua es, básicamente, cuando en un gráfico puedes realizar una representación gráfica de un solo trazo, sin levantar el lápiz.
Por su parte, una función real consiste en una función perteneciente a la variable real, es decir, compuesta por números reales (representados por la letra R). Un ejemplo de función real es:
F: f(x) R –> R
¿Quieres saber qué es el Teorema de Tales? Obtén más información ingresando aquí.
Un poco de historia
Este famoso teorema fue establecido por el matemático y filósofo checo Bernhard Bolzano. Fue reconocido por sus grandes aportes dentro de ambos campos de estudio. Habiendo desarrollado su carrera filosófica en la Universidad de Praga, donde nació.
Bolzano tuvo una historia interesante y, en parte, similar a lo ocurrido con el físico, astrónomo y matemático italiano Galileo Galilei, aunque sin compartir su mismo y brutal final. Durante un momento muy transcendental de su vida como profesional, se lo acusó de profesar ideas contrarias a la religión y política existente en ese momento. Se comenzó a censurar a todas sus obras.
A causa de ello, sus obras no causaron la repercusión que sí tuvieron años después. De hecho, fue muy criticado por la comunidad en sus años de vida. Al final, muchos años después, sus postulados y teorías fueron utilizados por otros intelectuales para desarrollar modelos, hipótesis y teoremas. Entre los intelectuales más reconocidos, se destacan: Weierstrass y Cantor.
Enunciado del Teorema de Bolzano
Su enunciado, literal, es el siguiente:
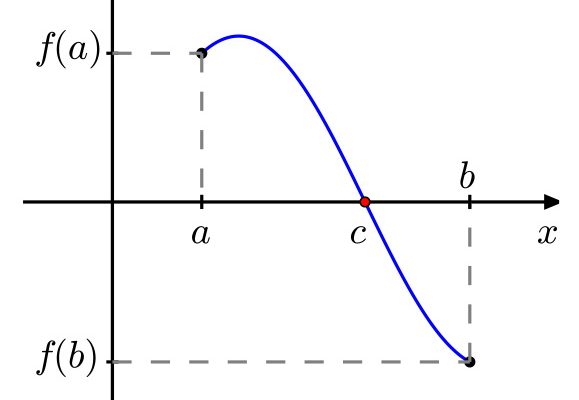
“Si una función f(x) está definida y es continua en un intervalo cerrado [a, b] y toma valores de distinto signo en los extremos a y b, entonces existe al menos un punto c del intervalo abierto (a, b) en el que se anula la función.”
Es decir, explicado de una manera más simplificada, significa que en toda función continua de intervalo cerrado con distintos valores (A y B) existe un punto (C), ubicado en el intervalo abierto, que anula la función, es decir, que es igual a 0. Esa unión entre los puntos A y B se ubica en el eje X, o, mejor dicho, en algún punto de ese eje.
Los intervalos abiertos se representan entre “()” y los cerrados con “[]”.
¿Cómo aplicar el Teorema de Bolzano?
Supongamos que tienes la función F(x) = x³ + x − 1 y la igualas a 0 (=0). Esta función, al ser polinómica, es continua y como resultado presenta un intervalo abierto entre los valores 0 y 1 (0,1).
- Punto A: f (0) = -1 < 0
- Punto B: f (1) = 1 > 0
- Punto C: f (c) = 0
Puedes conocer que en el lado negativo se determina que el punto A f (0) = -1< (eje inferior x) mientras que en la parte de arriba (lado positivo) se cumple que f (1) = 1>0, que es el punto B. Entonces, con esos datos y con base en lo que se establece con el Teorema de Bolzano, puedes determinar que el famoso punto C que buscabas se encuentra en 0, es decir, f(c) = 0.
Ejemplo de gráfico del Teorema de Bolzano
A continuación, te mostraremos un ejemplo detallado y gráfico del Teorema de Bolzano:
¿Necesitas ayuda con el Teorema de Bolzano?
En TFG Online somos conscientes que los teoremas matemáticos y todo lo relacionado con ese mundo no es para cualquiera. Si eres de los que se resisten a las matemáticas o simplemente no logras comprenderlo, podemos ofrecerte la mejor y más sencilla solución: contrata nuestro servicio. Contamos con los mejores y más profesionales redactores académicos especializados en todas las áreas y por supuesto que en estas temáticas.
Nuestro servicio te asegura total confidencialidad de tus datos personales y académicos, además de un proyecto redactado 100 % original libre de plagio académico. Utilizamos las mejores y profesionales herramientas para estar seguros de ello. Así como también podemos diseñar tus diapositivas y presentaciones para cuando debas rendir o defender otro tipo de proyectos.
¡Llenar el formulario de forma gratuita!
¡Pídenos tu presupuesto de forma gratuita y rápida! Solamente tienes que llenar el formulario web y nosotros nos moveremos para contactarte lo más rápido posible. Recuerda que nuestro servicio es personalizado porque tanto el tutor como el presupuesto que te asignamos son basándonos en el tipo y área del proyecto, además de sus tiempos de entrega.
¡Contamos con muchos y diversos medios de pago! Así que puedes optar y elegir la forma más cómoda de abonar nuestro servicio.












