Todo lo que necesitas saber sobre el Teorema de Rolle
Las matemáticas pueden ser complejas de comprender y más si no eres muy amante de las mismas. En este artículo en particular, te explicaremos qué es, para qué sirve, sus consideraciones y te daremos buenos ejemplos aplicados el Teorema de Rolle para que puedas aplicar a tu TFG, TFM o tesis doctoral (TD).
¿Qué es y para qué sirve el Teorema de Rolle?
El Teorema de Rolle es un enunciado matemático que toma su nombre del matemático francés Michel Rolle. Este fue uno de los primeros matemáticos en establecer y trabajar con el desarrollo del cálculo e inventor del famoso procedimiento conocido como eliminación gaussiana o de Gauss-Jordan.
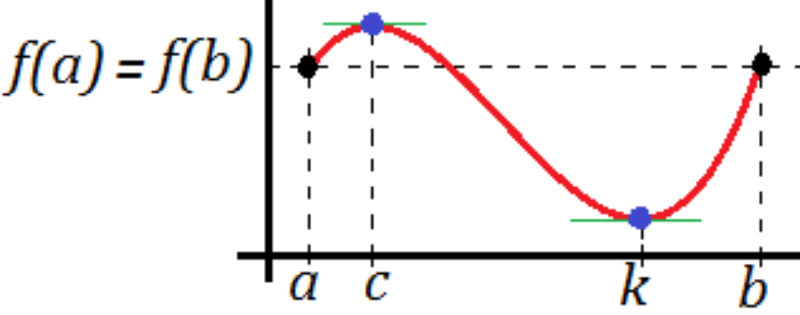
Este teorema te permitirá saber y afirmar si una función posee un punto crítico en un determinado intervalo. Es decir, enuncia que si, por ejemplo, la función f(x) es continua en el intervalo cerrado [a, b]; es derivable en el abierto (a, b) y los valores de sus extremos son iguales f(a) = f(b). Entonces, existen un punto c en el intervalo abierto (a, b) que vale anula a la derivada y vale 0 (f´(c) = 0).
Aquí un ejemplo gráfico:
Consideraciones
Algunas de las consideraciones a tener en cuenta sobre el Teorema de Rolle:
- A nivel gráfico, en el teorema, se encuentra que ese punto c se ubica en paralelo al eje x (abscisas) siempre y cuando se cumpla lo enunciado por el teorema mismo.
- Puede existir tanto un punto f´= 0 como varios más.
- SI se trata de una función constante, entonces cualquier punto del intervalo abierto (a, b) cumpliría con lo estipulado por el teorema.
Estas consideraciones te permitirán comprender mejor el uso y aplicación de Teorema de Rolle.
¿Quién fue Michel Rolle?
El creador del Teorema de Rolle fue el matemático francés Michel Rolle, que además fue autor de diversos estudios además del Teorema. Este gran matemático de la época no tuvo prácticamente una formación académica habitual, sino que se convirtió en un matemático por medio del estudio autodidacta.
El Teorema de Rolle vio la luz en el año 1682 para resolver un problema por otro matemático relevante de la época, Jacques Ozanam. Su publicación fue en el Journal des sçavans. Probablemente, su obra más relevante fue el Traité d’algèbre en 1690, donde descubrió una forma de representar la raíz n-ésima de un determinado número: n√x, que sigue siendo aplicada hoy en día.
De manera definitiva, fue presentado el teorema hecho para polinomios y no basado en el cálculo diferencial. Se publicó en el año 1691 y ha tenido positivas aceptaciones por parte de la comunidad científica y matemática, pese a la nula preparación académica convencional de la que venía Rolle.
Ejemplo de uso del Teorema de Rolle
Ahora vamos a darte un ejemplo del uso del Teorema de Rolle para que comprendas la idea de manera más práctica:
Vamos con el primer ejemplo:
Lo primero que se pide es que halles el punto j para que la función h cumpla lo establecido por Rolle en el intervalo cerrado [0, j].
Debes comenzar así:
h(x) = x^2 – 4x + 5
Esta es una función polinómica, así que la continuidad y su derivabilidad no te pueden suponer complicaciones.
Ahora bien, analicemos las condiciones:
- h (0) = h(j).
- Si h (0) = 5, entonces tienes que buscar j>0, de modo que h(j) = 5.
- La ecuación se resuelve haciendo lo del principio: h (0) = h(j).
h(j) = 5
j^2 + 4j + 5 = 5
j^2 – 4j = 0
j (j-4) = 0
j = 0, j = 4
De ese modo, el resultado obtenido te deja con el intervalo [0,4]. Ahora, a continuación, debes obtener el famoso punto c, que es el que se anula en 0 según el Teorema de Rolle. Para obtenerlo, debes calcular la derivada, igualando a 0 y realizando la ecuación:
g´(x) = 2x – 4
2x – 4 = 0
2x = 4
x = 2
Entonces, c se anula en 2, y se cumple el Teorema de Rolle.
Teorema de Rolle con Weierstrass
Ahora vamos a darte un ejemplo bastante más complejo, combinando el Teorema de Rolle con el de Weierstrass:
Tienes a x como un punto interior perteneciente al intervalo cerrado [a, b]. La función es continua en un compacto cerrado por el Teorema de Weierstrass, así que vas a tener dos puntos en el mismo intervalo: x e y. (Xo, Yo E [a, b]). Esto con la finalidad de que f llegue a valores extremos absolutos:
F(Xo) ≤ F(X) ≤ F(Yo),
∀xE [a, b]
Si se da que Xo es un punto interior del intervalo, sin ser a o b, entonces si es un extremo de esta función. Con esto, podemos considerar al punto C=Xo. Lo mismo corre para el punto Yo.
Ahora bien, de no ser ese el caso, la solución sería pensar que tanto Xo e Yo son los extremos del intervalo cerrado. Suponiendo que a = Xo y b = Yo, quedando:
F(a) ≤ F (x) ≤ F(b),
∀xE [a, b]
Como a y b son iguales, entonces la función es constante, su derivada se anula y se completa el postulado del Teorema de Rolle.
¿Necesitas ayuda para realizar correctamente el Teorema de Rolle?
En TFG Online sabemos que realizar este tipo de cálculos matemáticos puede ser complejo, más si no es de tu mayor agrado. Si desde la universidad te han pedido realizar un proyecto basándonos en el Teorema de Rolle y no sabes qué hacer, no te preocupes. ¡Podemos ayudarte! Contamos con un excelente cuerpo de profesionales especializados en todas las áreas de la matemática y redacción académica.
Aplicamos las mejores herramientas con la finalidad de prevenir el plagio académico de tu proyecto y además te garantizamos total confidencialidad de tus datos personales. Recuerda que nuestro servicio es personalizado, así que podemos ofrecerte un presupuesto y tutor a tu medida y la del proyecto que traigas.
¡No dudes y solicita tu presupuesto gratuito!
Solo tienes que llenar el formulario y podres comunicarnos contigo lo antes posible para que puedas solicitar tu presupuesto totalmente gratuito y sin obligación de compra. Además, contamos con múltiples medios de pago para que puedas abonar el servicio de la manera que sea más cómoda para ti y tu economía.