Teorema de Pitágoras: te explicamos todo lo que necesitas saber
El Teorema de Pitágoras es una ecuación muy conocida y que muchos pueden utilizar de manera adecuada para su TFG, TFM o tesis doctoral. Aunque, si eres de los que no se llevan bien con las matemáticas, quizás no la tengas tan fácil. En este post te explicaremos qué es, la historia, la formula y cómo aplicarlo. Además, te daremos buenos ejemplos del Teorema de Pitágoras.
¿Qué es el Teorema de Pitágoras?
Se define al Teorema de Pitágoras como la relación existente entre todos los lados del triángulo rectángulo, que un poco más adelante te explicaremos qué es. Este famoso teorema establece que el área de un cuadrado que posea el lado más largo del triángulo rectángulo siempre va a ser igual a la suma que se realice entre las áreas de los cuadrados que formes con los otros lados menores del triángulo.
Un triángulo rectángulo es un polígono que tiene tres lados y forma un ángulo de 90°, siendo también conocido como un ángulo recto. Al tener tres lados, los dos iguales son los catetos, mientras que el más largo es la hipotenusa. Con base en ello, el teorema de Pitágoras asegura que la suma de los catetos al cuadrado siempre será igual a la hipotenusa.
¿Quieres saber más sobre el Teorema de Bolzano? Ingresa a este artículo para averiguarlo.
¿Quién fue Pitágoras?
Ahora bien, ¿qué fue de la vida de Pitágoras? La figura de este matemático es un enigma en ciertos aspectos, ya que se sabe realmente poco y fueron los mismos pitagóricos, culto religioso que lo venera, quienes asumen dichos misterios sobre el mismo.
Pitágoras fue un filósofo y matemático griego nacido en la Isla de Samos, entre los años 582 y 500 a.C. Su formación académica fue influenciada por los primeros filósofos más conocidos, como lo fueron Anaximandro; Anaxímenes y Tales de Mileto. Algunas fuentes afirman que había sido condenado y exiliado por su confrontación a la tiranía de Polícrates.
Más tarde, a la edad de 30 años, se instaló en Crotona, una ciudad italiana. Ahí fundó un movimiento de políticos y religiosos filósofos que lo seguirían a todos lados, los orígenes de los pitagóricos.
Entre las mil y una teorías y misterios sobre las creencias religiosas y políticas de Pitágoras y su gente, se destacan sus investigaciones matemáticas sobre los estudios de números pares e impares; de los números primos y cuadrados y la teoría de los números. Se desarrolló, gracias a sus estudios, el concepto de número, gracias a lo cual se desarrolló una amplia gama de estudios y bases científicas para las matemáticas.
El Teorema de la hipotenusa, también conocido como el Teorema de Pitágoras, fue y es el mayor descubrimiento de la escuela pitagórica en cuanto a lo aritmético.
Ejemplos
La fórmula, que es una ecuación, principal del teorema es la siguiente:
a^2 + b^2 = c^2 (donde a y b son los catetos y c es la hipotenusa, los tres se encuentran al cuadrado)
Otro ejemplo que puede aplicar es el más común y utilizado de todos: la escalera y la pared. Supongamos que tienes que reparar una pared, y utilizas la escalera para subir. Con la ecuación de Pitágoras, puedes calcular la longitud de la escalera, que actúa como hipotenusa frente a la pared y el piso, que fungen como los catetos.
Datos: la pared mide 3 metros, la escalera está a 50 centímetros de la pared. ¿Cuán alta es la escalera? Ahora lo resolvemos:
a^2 + b^2 = c^2
Todas las unidades deben estar en la misma medida, así que pasaremos los metros a centímetros.
(300cm) ^2 + (50cm) ^2 = c^2
c = √(300cm) ^2 + (50cm) ^2
c = aproximadamente 304 centímetros.
Aquí te dejamos un ejemplo de aplicación sencillo del Teorema de Pitágoras:
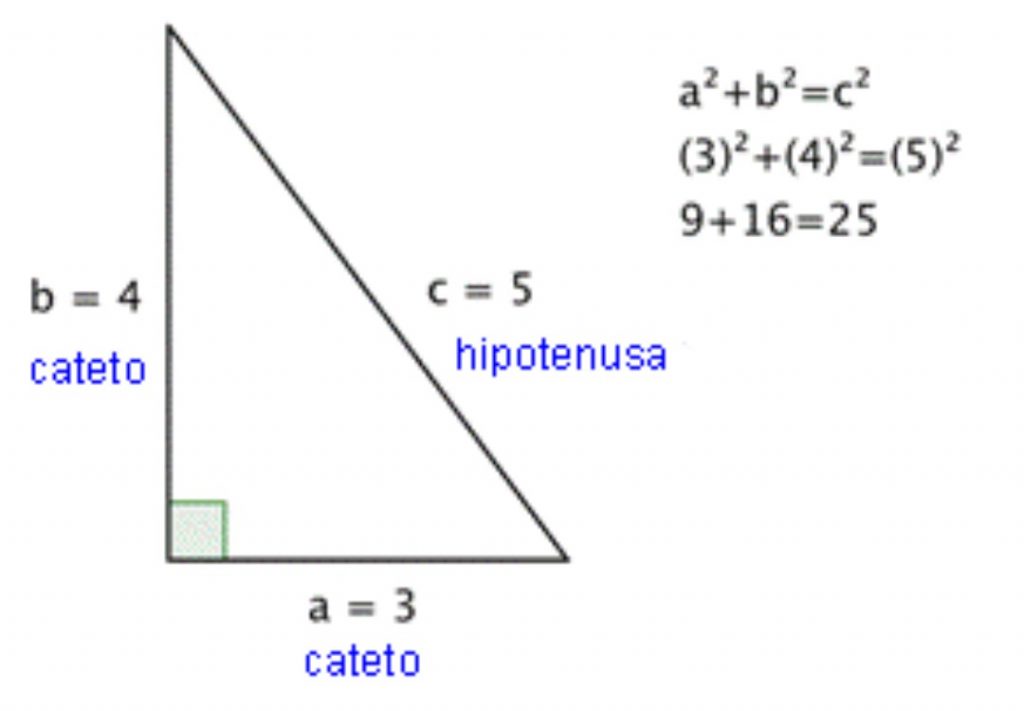
Aplicación
El Teorema de Pitágoras puede ser aplicado a muchos otros campos y disciplinas, incluso oficios y trabajos, como, por ejemplo:
- Física: en física se puede aplicar este teorema para realizar cálculos diferenciales.
- Arquitectura: tanto en arquitectura; carpintería; construcción y otras áreas, el Teorema de Pitágoras se utiliza para, por ejemplo, conocer la altura de un techo o la distancia que debe cubrir. Las vigas diagonales también se cortan por medio del cálculo de este teorema.
- Navegación: en este último segmento, el cálculo es aplicado para conocer cuáles son las rutas de navegación más cortas.
El teorema puede aplicarse a muchas otras actividades, incluso a quehaceres de la vida cotidiana que manejes. Lo importante de esta ecuación es que te permite medir distancias y alturas que necesites siempre y cuanto se cumplan los requisitos previos que exige tanto el teorema como la definición misma de los triángulos rectángulos.
¿Necesitas ayuda con tus proyectos académicos?
En TFG Online sabemos que la utilización de ecuaciones, fórmulas y diversos cálculos matemáticos no son para cualquiera. O, mejor dicho, si no te gustan puede que lo encuentres más complicado que el resto. Podemos ayudarte con eso, ya que nuestro equipo se encuentra compuesto por múltiples especialistas y profesionales en el otro de las matemáticas y la estadística.
Utilizamos las mejores herramientas y aplicaciones para evitar el plagio académico. Te garantizamos total confidencialidad con tus datos personales y un servicio personalizado porque nos ajustamos a tus necesidades, tiempos y tipo de proyecto para asignarte al tutor y el presupuesto.
¡Solicítanos un presupuesto gratuito!
Solo tienes que completar el formulario web y nosotros te contactaremos lo antes posible. Nuestro presupuesto es fácil, rápido y gratuito, la mejor combinación posible. Adicionalmente, te recordamos que contamos con múltiples medios de pago para que puedas abonar el servicio, así puedes sentirte con total comodidad financiera.
¡No dudes más y da el paso final para concluir tu proyecto del Teorema de Pitágoras!