Te contamos todo lo que necesitas conocer sobre el Teorema de Tales
Si te encuentras buscando la información más completa sobre los Teoremas de Tales, ¡buena noticia! Aquí te detallaremos todo lo que necesitas saber sobre este tema para formularlo de forma correcta.
En este post te contaremos la definición, un ejemplo, y la extensión del teorema de tales, ¿comenzamos?
¿Qué es el Teorema de Tales?
El teorema de Tales es una ley, que forma parte de la geometría. Indica que si realizas una línea paralela a cualquiera de los lados de, por ejemplo: un triángulo, tendrás como resultado un triángulo similar al original.
En otras palabras, si cortas un triángulo dibujando una línea paralela a uno de sus lados, obtendrás un triángulo igual al anterior existente.
Cabe destacar, que dos triángulos son similares cuando sus ángulos correspondientes miden lo mismo, y sus lados son proporcionales entre sí.
A continuación, te mostraremos un ejemplo para que lo comprendas mejor:
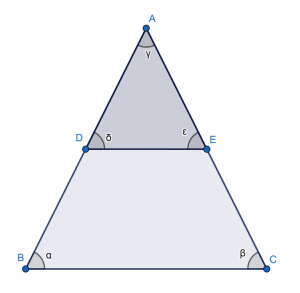
Por el teorema de Tales se puede decir que α=δ y β=ε
Como mencionamos anteriormente, los lados son proporcionales, cumpliendo lo siguiente:
AB/AD = AE/AC = DE/BC
Historia del teorema de Tales
El historiador Plutarco, cuenta la anécdota que Tales de Mileto, en uno de sus tantos viajes, realizó este teorema. Su objetivo era hallar la altura de las pirámides de Guiza, las de Micerino, Kefrén y Keops, en Egipto.
Así, decidió colocar una vara de forma vertical contra el suelo, Tales esperaba que la longitud del objeto sea igual a la sombra que éste proyectaba.
En ese momento, la sombra que se veía en la pirámide también sería semejante a la altura de esta.
En este caso, los triángulos similares son:
- El que tiene dos lados. Un lado la vara, y en otro la sombra.
- Triángulo que, en uno de sus lados, posee la altura de la pirámide, mientras que, de otro lado, se proyecta la sombra de esta.
Segundo teorema de Tales
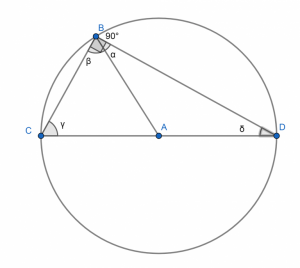
Existe el segundo teorema de Tales. Si tienes un triángulo conformado por el diámetro de una determinada circunferencia y, además, dos rectas secantes (cortando la figura en dos puntos); dicho ángulo que se encuentra frente al diámetro es lineal, en otras palabras, mide 90º.
Recordemos que un diámetro es un segmento que, atravesando el centro de la circunferencia, une dos puntos opuestos, pero que pertenecen a la misma figura.
Este teorema de Tales lo puedes comprobar teniendo en cuenta que AC, AD y AB son iguales al radio de la circunferencia y miden exactamente lo mismo.
El radio es cualquier tipo de segmento que une un determinado punto de la circunferencia con el centro de la figura, dicho punto representa a la mitad del diámetro.
Entonces, los ángulos ABC y ABD tienen sus dos lados similares y al mismo tiempo opuestos a algunos, que miden lo mismo, son isósceles. Esto quiere decir que:
AC = AD = AB = r (radio de la circunferencia)
γ=β y α=δ
Después, si ves el alguno CBD y recuerdas que los ángulos internos de un triángulo tienen que sumar 180º, debes realizar lo siguiente:
γ+β +α+δ =180º
2β+2α =180º
2(α+β) =180º
α+β= 90º
Por lo tanto, el triángulo CBD representa a un triángulo rectángulo.
Ejemplo del teorema de Tales
Para un mayor entendimiento sobre el teorema de Tales, a continuación, observa nuevamente la primera figura.
Supongamos que BC mide 7,3 metros. Los lados DE miden 3,6 metros y AB mide 6,2 metros. La pregunta es, ¿cuál es la longitud que tiene AD?
Entonces, lo que debes hacer primero es despejar según la fórmula mostrada anteriormente, y luego debes realizar lo siguiente:
7,3/3,6=6,2/AD
2,0278=6,2/AD
AD=3,0575 metros
Extensión del teorema de Tales
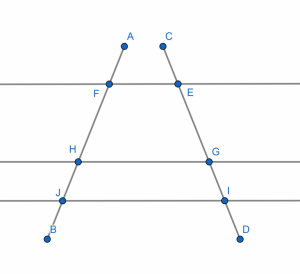
El teorema de Tales puede extenderse al estudio de dos rectas cualquieras que son cortadas por otras dos líneas paralelas entre sí. Seguidamente, observa la imagen:
Entonces, podemos ver que se cumple lo siguiente:
FH/EG = HJ/GI = FJ/EI
Lo visto previamente se cumple porque debes pensar en esas líneas como parte de una figura geométrica, en este caso el triángulo.
Viéndolo de otra manera, si extiendes las rectas AB y CD, estas evidentemente se cruzaran.
¿Necesitas ayuda para tus trabajos académicos?
En TFG Online podemos ayudarte a realizar todos tus proyectos académicos, como tu TFG, TFM, tu programación didáctica, unidad didáctica, presentaciones, y ¡hasta tu tesis doctoral!
Contamos con más de 500 profesionales capacitados para guiarte en todo el proceso de tus trabajos, desde la elección del tema, hasta la presentación final.
Además, trabajamos bajo las políticas de confidencialidad y seguridad de datos más rigurosas del país. Por lo tanto, tus datos están en buenas manos.
Pide tu presupuesto sin compromiso
Completa el siguiente formulario que verás a continuación. En breve, un asesor de nuestro equipo se pondrá en contacto contigo para realizarte un presupuesto pensado para tus necesidades. ¡Estás a un clic de distancia para alcanzar tus objetivos académicos!